r = 1 #假设半径为1# 0~2π(一圈,一个π是半圈,步长=0.01,步长越小图线越平滑)a = np.arange(0,2np.pi,0.01) #圆的坐标点与三角函数的关系x = rnp.cos(a)y = rnp.sin(a)#画圆plt.plot(x,y,color='red')3.sin正弦函数3.1 静态:sin-s3.2 代码:简洁版#---导出模块---import matplotlib.pyplot as pltimport numpy as np#定义坐标关系x = np.arange(-2np.pi,2np.pi,0.1)y = np.sin(x)#画线plt.plot(x,y,color='blue')plt.title('sin-s') #标题plt.legend(['sin']) #图例,注意中括号plt.show() #图片展示3.3 图sin-s-13.4 代码:注释版#---导出模块---import matplotlib.pyplot as pltimport numpy as np#---定义画布大小和分辨率#fig = plt.figure(figsize=(8,8),dpi=80) #自定义#fig = plt.figure() #这是默认的,也可以这一行不设,就是默认#---画正弦sin曲线---#0.001越小,线条越平滑好看#从-2np.pi到2np.pi=就是2个2π,4个波=2个波峰+2个波底#x = np.arange(-2np.pi,2np.pi,0.001)x = np.arange(-2np.pi,2np.pi,0.1)y = np.sin(x)#画线plt.plot(x,y,color='blue')#默认显示2个2π,4个波=2个波峰+2个波底#plt.ylim(-2, 2)#plt.xlim(-2, 2)plt.title('sin-s') #标题plt.legend(['sin']) #图例,注意中括号plt.show() #图片展示4.cos余弦函数:4.1 将上面的sin函数的简洁版的代码中,sin改为cos即可,颜色定义为绿色=green。4.2 代码:简洁版#---导出模块---import matplotlib.pyplot as pltimport numpy as np#---画正弦cos曲线---x = np.arange(-2np.pi,2np.pi,0.1)y = np.cos(x)#画线plt.plot(x,y,color='green')plt.title('cos-s') #标题plt.legend(['cos']) #图例,注意中括号plt.show() #图片展示4.3 图:cos-s-15.一个坐标系展示sin和cos作图法5.1 代码1:#---导出模块---import matplotlib.pyplot as pltimport numpy as np#plt.figure() #可以不要,采用默认#取值范围-2π~2π,比较能展现sin和cos的特点#0.1~0.001,最好越小越好,线条越平滑x=np.arange(-2np.pi,2np.pi,0.1)y1=np.sin(x) #正弦sin函数线条y2=np.cos(x) #余弦cos函数线条#绘制两个图形,需要绘制两次#不设置颜色,采用默认的2种不同颜色,也可以单独设置颜色#本讲解中sin设置蓝色=blue,cos设置为绿色=greenplt.plot(x,y1,color='blue')plt.plot(x,y2,color='green')#增加标题plt.title('x‘sin and cos')#增加图例plt.legend(['y=sinx','y=cosx'])#增加x轴和y轴标签名plt.xlabel('x-v')plt.ylabel('y-v',rotation=0)#图片展示plt.show()5.2 图:sin-cos-s-15.3 升级版,代码:#---导出模块---import numpy as npfrom matplotlib import pyplot as plt#---sin和cos的坐标值定义---#---注意np的arrange和linspace的含义,在这里区别不大##在-np.pi~np.pi之间选择256个等差数#x = np.linspace(-2np.pi, 2np.pi, 512, endpoint=True)x =np.arange(-2np.pi,2np.pi,0.001)#y1=sin,y2=cosy1, y2 = np.sin(x), np.cos(x)#定义画布大小,不设置就是默认#plt.figure(figsize=(10, 7))#取出一张107的白纸#画sin和cos,自定义颜色blue和green,label="sin",label="cos"plt.plot(x, y1, "-", color='blue',lw=2, aa=False, ms=50)#设置线宽5 aa关闭抗锯齿 默认开启plt.plot(x, y2, "-", color='green',lw=2, aa=True)#默认线宽10,不设置就是默认#去掉就是默认#自定义刻度法,取最大值×1.2plt.xlim(x.min() 1.2, x.max() 1.2)#横坐标范围plt.ylim(y1.min() 1.2, y1.max() 1.2)#纵坐标范围plt.xticks([0, x.max(), x.min()], [0, r"$\pi$", "$-\pi$"])#横坐标刻度plt.yticks([y1.min(), y1.max()])#纵坐标刻度#图例个性设置,自定义字体大小,位置默认是最佳,显示内容是label内容#也可以这样plt.legend(['sin','cos'],fontsize=20)#plt.legend(fontsize=20) #如何这样的话,那么需要在上面加入label#标注设置t = 2 / 3 np.pi#标注蓝色点垂直线plt.plot([t, t], [0, np.sin(t)], "--", color="b")plt.scatter([t], [np.sin(t)], s=100)#散点图#标注红色点垂直线plt.plot([t, t], [0, np.cos(t)], "--", color="r")plt.scatter([t], [np.cos(t)], s=100)#散点图#设置标注plt.annotate(r"$\sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$", (t, np.sin(t)), xycoords="data", textcoords="offset pixels", xytext=(20, 20), arrowprops=dict(arrowstyle="->" , connectionstyle="arc3,rad=.2"),#箭头属性 fontsize=16,#zi字体大小 )#设置标注plt.annotate(r"$\cos(\frac{2\pi}{3})=-\frac{1}{2}$", (t, np.cos(t)), xycoords="data", textcoords="offset pixels", xytext=(20, 0), arrowprops=dict(arrowstyle="->" , connectionstyle="arc3,rad=.2"),#箭头属性 fontsize=16,#zi字体大小 )#ax定义和边框线,也可以注释掉,那就是默认ax = plt.gca()#去除图片的四边黑框线ax.spines["bottom"].set_position(("data", 0))ax.spines["left"].set_position(("data", 0))ax.spines["top"].set_color("none")ax.spines["right"].set_color("none")#图片展示plt.show()5.4 图:sin-cos-s-25.5 豪华版代码:#---导出模块---import numpy as npimport matplotlib.pyplot as plt#---函数定义和画函数线---#x坐标的取值范围:linspace是等差数列法x=np.linspace(-2np.pi,2np.pi,256,endpoint=True)#arrange法,因为0.001取值很小很平滑,所以可能☆就不能显示#x =np.arange(-2np.pi,2np.pi,0.001)#定义余弦函数正弦函数,一行定义法,也可以y1和y2c,s=np.cos(x),np.sin(x)#画三角函数曲线,以x为横坐标,以s和c为纵坐标#plt.plot(x,s,"r",label="sin-s-3") #r=red的,相当于color='red',linestyle=""plt.plot(x,s,color="blue",label="sin-s-3")plt.plot(x,c,color="green",linestyle="-",label="cos-s-3",alpha=0.5)ax=plt.gca()#去除图片的四边的边框黑线ax.spines["right"].set_color("none")ax.spines["top"].set_color("none")ax.spines["left"].set_position(("data",0))ax.spines["bottom"].set_position(("data",0))#自定义标签文字#x轴标签依次是:,如果注释掉就是-6~6,间隔2plt.xticks([-np.pi,-np.pi/2,0,np.pi/2,np.pi],[r'$-\pi$',r'$-\pi/2$',r'$0$',r'$+\pi/2$',r'$+\pi$'])#y轴的标签,取值从-1~1,分5个等差plt.yticks(np.linspace(-1,1,5,endpoint=True))#默认标签位置也是这样,所以可以不要,注释掉#ax.xaxis.set_ticks_position("bottom") #线下#ax.yaxis.set_ticks_position("left") #线左边'''#如果上面的2行注释掉,那么下面的存在意义不大,也可以注释掉for label in ax.get_xticklabels()+ax.get_yticklabels(): label.set_fontsize(16) label.set_bbox(dict(facecolor="white",edgecolor="None",alpha=0.2))'''#固定面积显示plt.fill_between(x,np.abs(x)<0.5,c,c>0.5,color="yellow",alpha=0.25)#固定垂直虚线标注t=1plt.plot([t,t],[0,np.cos(t)],"y",linewidth=3,linestyle="--")#箭头标注plt.annotate("cos(1)",xy=(t,np.cos(1)),xycoords="data",xytext=(+10,+30),textcoords="offset points",arrowprops=dict(arrowstyle="->",connectionstyle="arc3,rad=.2"))#增加标题plt.title("sin-cos-s-3")#plt.figure(1) #可以注释掉,采用默认#图例显示,loc代表位置,这是固定左上角位置,默认best,最佳位置,可以自动调节空挡显示plt.legend(loc="upper left")#显示网格,可以注释掉plt.grid()#显示图形plt.show()5.6 图:sin-cos-s-36 sin和cos的布局6.1 ggplot法,代码:#导出模块import numpy as npimport matplotlib.pyplot as plt#画布采用默认大小fig=plt.figure() #采用ggplot法布局三个图片位置plt.style.use('ggplot')left,width = 0.05,0.95#位置布局一:上面一行2个rect_sin=[left,0.55,0.45,0.3] #第1个图rect_cos=[left+0.5,0.55,0.45,0.3] #第2个图'''#位置布局二:上下2个,靠左rect_sin=[left,0.55,0.45,0.3] #第1个图rect_cos=[left,0.1,0.45,0.3] #第2个图'''#定义x和y坐标#x=np.linspace(-10,10) #未设置等分,则线条不平滑#x=np.linspace(-10,10,260) #260等分,数值越大,曲线的线条越平滑x=np.arange(-10,10,0.001) #arange则是0.001,越小越平滑#y1=np.sin(x)#y1=np.cos(x)#---第1个图---正弦sinax_sin = fig.add_axes(rect_sin)ax_sin.plot(x,np.sin(x),color='blue')ax_sin.set_title('Sin-s-ggplot')#---第2个图---余弦cosax_cos=fig.add_axes(rect_cos)ax_cos.plot(x,np.cos(x),color='green')ax_cos.set_title('Cos-s-ggplot')#图片展示plt.show()图:2lf-ggplot法2ud-ggplot法图6.2 subplot法代码:#---导出模块---import matplotlib.pyplot as pltimport numpy as np#---定义画布大小和分辨率---fig = plt.figure(figsize=(8,8),dpi=80)#采用subplot法,分四个图#2,2,1=2行2列,第一个,从左边数# 画正弦曲线fig.add_subplot(2,2,1)x = np.arange(-2np.pi,2np.pi,0.001)y = np.sin(x)plt.plot(x,y,color='blue')plt.title('Sin-s-subplot')plt.legend(['sin'])#方法一:第1行1和2并列# 余弦,2,2,2=2行2列,第2个,从左边数#fig.add_subplot(2,2,2)#方法二:第1行1和第2行1,上下# 余弦,2,2,2=2行2列,第2个,从左边数fig.add_subplot(2,2,3)x = np.arange(-2np.pi,2np.pi,0.001)y = np.cos(x)plt.plot(x,y,color='green')plt.title('Cos-s-subplot')plt.legend(['cos'])plt.show()6.3 图略,作图位置如上面的ggplot法。7.小结:7.1 学习sin和cos有没有用,当然有,在画圆中需要sin和cos来定位圆的坐标。基础一定要打好。7.2 顺带复习matplotlib的相关作图。7.3 我自己整理好,也分享出来,值得收藏。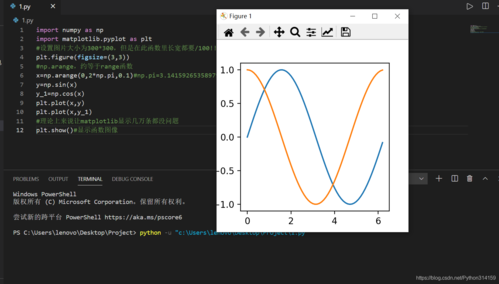
(图片来源网络,侵删)








0 评论