前方高能
需要你有一些基本的多元函数微分知识,比如偏导数、链式求导法则)如果调整一下w1,损失函数是会变大还是变小?我们需要知道偏导数∂L/∂w1是正是负才能回答这个问题根据链式求导法则:而L=(1-ypred)2,可以求得第一项偏导数:接下来我们要想办法获得ypred和w1的关系,我们已经知道神经元h1、h2和o1的数学运算规则:实际上只有神经元h1中包含权重w1,所以我们再次运用链式求导法则:然后求∂h1/∂w1我们在上面的计算中遇到了2次激活函数sigmoid的导数f′(x),sigmoid函数的导数很容易求得:总的链式求导公式:这种向后计算偏导数的系统称为反向传播(backpropagation)上面的数学符号太多,下面我们带入实际数值来计算一下h1、h2和o1h1=f(x1⋅w1+x2⋅w2+b1)=0.0474h2=f(w3⋅x3+w4⋅x4+b2)=0.0474o1=f(w5⋅h1+w6⋅h2+b3)=f(0.0474+0.0474+0)=f(0.0948)=0.524神经网络的输出y=0.524,没有显示出强烈的是男(1)是女(0)的证据现在的预测效果还很不好我们再计算一下当前网络的偏导数∂L/∂w1:这个结果告诉我们:如果增大w1,损失函数L会有一个非常小的增长随机梯度下降下面将使用一种称为随机梯度下降(SGD)的优化算法,来训练网络经过前面的运算,我们已经有了训练神经网络所有数据但是该如何操作?SGD定义了改变权重和偏置的方法:η是一个常数,称为学习率(learning rate),它决定了我们训练网络速率的快慢将w1减去η·∂L/∂w1,就等到了新的权重w1当∂L/∂w1是正数时,w1会变小;当∂L/∂w1是负数 时,w1会变大如果我们用这种方法去逐步改变网络的权重w和偏置b,损失函数会缓慢地降低,从而改进我们的神经网络训练流程如下:1、从数据集中选择一个样本;2、计算损失函数对所有权重和偏置的偏导数;3、使用更新公式更新每个权重和偏置;4、回到第1步我们用Python代码实现这个过程:import numpy as npdef sigmoid(x): # Sigmoid activation function: f(x) = 1 / (1 + e^(-x)) return 1 / (1 + np.exp(-x))def deriv_sigmoid(x): # Derivative of sigmoid: f'(x) = f(x) (1 - f(x)) fx = sigmoid(x) return fx (1 - fx)def mse_loss(y_true, y_pred): # y_true and y_pred are numpy arrays of the same length. return ((y_true - y_pred) 2).mean()class OurNeuralNetwork: ''' A neural network with: - 2 inputs - a hidden layer with 2 neurons (h1, h2) - an output layer with 1 neuron (o1) DISCLAIMER : The code below is intended to be simple and educational, NOT optimal. Real neural net code looks nothing like this. DO NOT use this code. Instead, read/run it to understand how this specific network works. ''' def __init__(self): # Weights self.w1 = np.random.normal() self.w2 = np.random.normal() self.w3 = np.random.normal() self.w4 = np.random.normal() self.w5 = np.random.normal() self.w6 = np.random.normal() # Biases self.b1 = np.random.normal() self.b2 = np.random.normal() self.b3 = np.random.normal() def feedforward(self, x): # x is a numpy array with 2 elements. h1 = sigmoid(self.w1 x[0] + self.w2 x[1] + self.b1) h2 = sigmoid(self.w3 x[0] + self.w4 x[1] + self.b2) o1 = sigmoid(self.w5 h1 + self.w6 h2 + self.b3) return o1 def train(self, data, all_y_trues): ''' - data is a (n x 2) numpy array, n = # of samples in the dataset. - all_y_trues is a numpy array with n elements. Elements in all_y_trues correspond to those in data. ''' learn_rate = 0.1 epochs = 1000 # number of times to loop through the entire dataset for epoch in range(epochs): for x, y_true in zip(data, all_y_trues): # --- Do a feedforward (we'll need these values later) sum_h1 = self.w1 x[0] + self.w2 x[1] + self.b1 h1 = sigmoid(sum_h1) sum_h2 = self.w3 x[0] + self.w4 x[1] + self.b2 h2 = sigmoid(sum_h2) sum_o1 = self.w5 h1 + self.w6 h2 + self.b3 o1 = sigmoid(sum_o1) y_pred = o1 # --- Calculate partial derivatives. # --- Naming: d_L_d_w1 represents \"partial L / partial w1\" d_L_d_ypred = -2 (y_true - y_pred) # Neuron o1 d_ypred_d_w5 = h1 deriv_sigmoid(sum_o1) d_ypred_d_w6 = h2 deriv_sigmoid(sum_o1) d_ypred_d_b3 = deriv_sigmoid(sum_o1) d_ypred_d_h1 = self.w5 deriv_sigmoid(sum_o1) d_ypred_d_h2 = self.w6 deriv_sigmoid(sum_o1) # Neuron h1 d_h1_d_w1 = x[0] deriv_sigmoid(sum_h1) d_h1_d_w2 = x[1] deriv_sigmoid(sum_h1) d_h1_d_b1 = deriv_sigmoid(sum_h1) # Neuron h2 d_h2_d_w3 = x[0] deriv_sigmoid(sum_h2) d_h2_d_w4 = x[1] deriv_sigmoid(sum_h2) d_h2_d_b2 = deriv_sigmoid(sum_h2) # --- Update weights and biases # Neuron h1 self.w1 -= learn_rate d_L_d_ypred d_ypred_d_h1 d_h1_d_w1 self.w2 -= learn_rate d_L_d_ypred d_ypred_d_h1 d_h1_d_w2 self.b1 -= learn_rate d_L_d_ypred d_ypred_d_h1 d_h1_d_b1 # Neuron h2 self.w3 -= learn_rate d_L_d_ypred d_ypred_d_h2 d_h2_d_w3 self.w4 -= learn_rate d_L_d_ypred d_ypred_d_h2 d_h2_d_w4 self.b2 -= learn_rate d_L_d_ypred d_ypred_d_h2 d_h2_d_b2 # Neuron o1 self.w5 -= learn_rate d_L_d_ypred d_ypred_d_w5 self.w6 -= learn_rate d_L_d_ypred d_ypred_d_w6 self.b3 -= learn_rate d_L_d_ypred d_ypred_d_b3 # --- Calculate total loss at the end of each epoch if epoch % 10 == 0: y_preds = np.apply_along_axis(self.feedforward, 1, data) loss = mse_loss(all_y_trues, y_preds) print(\"Epoch %d loss: %.3f\" % (epoch, loss))# Define datasetdata = np.array([ [-2, -1], # Alice [25, 6], # Bob [17, 4], # Charlie [-15, -6], # Diana])all_y_trues = np.array([ 1, # Alice 0, # Bob 0, # Charlie 1, # Diana])# Train our neural network!network = OurNeuralNetwork()network.train(data, all_y_trues)随着学习过程的进行,损失函数逐渐减小现在我们可以用它来推测出每个人的性别了:# Make some predictionsemily = np.array([-7, -3]) # 128 pounds, 63 inchesfrank = np.array([20, 2]) # 155 pounds, 68 inchesprint(\"Emily: %.3f\" % network.feedforward(emily)) # 0.951 - Fprint(\"Frank: %.3f\" % network.feedforward(frank)) # 0.039 - M更多这篇教程只是万里长征第一步,后面还有很多知识需要学习:1、用更大更好的机器学习库搭建神经网络,如Tensorflow、Keras、PyTorch2、在浏览器中的直观理解神经网络:https://playground.tensorflow.org/3、学习sigmoid以外的其他激活函数:https://keras.io/activations/4、学习SGD以外的其他优化器:https://keras.io/optimizers/5、学习卷积神经网络(CNN)6、学习递归神经网络(RNN)这些都是Victor给自己挖的“坑”他表示自己未来“可能”会写这些主题内容,希望他能陆续把这些坑填完如果你想入门神经网络,不妨去订阅他的博客关于这位小哥Victor Zhou是普林斯顿2019级CS毕业生,已经拿到Facebook软件工程师的offer,今年8月入职他曾经做过JS编译器,还做过两款页游,一个仇恨攻击言论的识别库最后附上小哥的博客链接:https://victorzhou.com/— 完 —诚挚招聘量子位正在招募编辑/记者,工作地点在北京中关村期待有才气、有热情的同学加入我们
相关细节,请在量子位公众号(QbitAI)对话界面,回复“招聘”两个字量子位 QbitAI · 头条号签约作者վ'ᴗ' ի 追踪AI技术和产品新动态
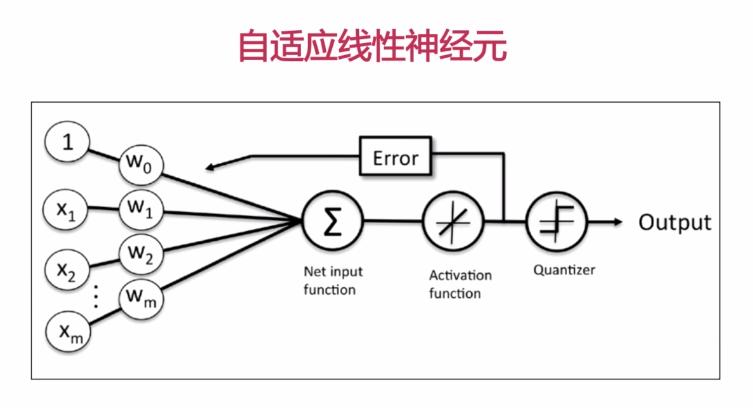
(图片来源网络,侵删)







0 评论